Bardzo duży magnes - pomiar ziemskiego pola magnetycznego
Poniższy artykuł został opublikowany pierwotnie w czasopiśmie dla nauczycieli Fizyka w Szkole (6/2017):

Fenomen magnetyzmu nie jest w swej istocie jednorodny - pojęciem tym określamy cały zespół zjawisk fizycznych związanych z polem magnetycznym. Pole to może być wytwarzane przez materiały magnetyczne, ale też poprzez przepływ prądu elektrycznego.
Na podstawie wykazywanych własności magnetycznych mogą zostać sklasyfikowane wszystkie znane substancje, tj. pierwiastki, związki chemiczne i materiały złożone. Dodatkowo każdy pierwiastek chemiczny wykazuje jeden z czterech podstawowych typów magnetyzmu: diamagnetyzm, paramagnetyzm, ferromagnetyzm lub ferrimagnetyzm.
W praktyce największe zastosowanie znalazły ferromagnetyki, które można podzielić na materiały magnetycznie twarde używane jako magnesy trwałe, miękkie wykorzystywane do produkcji np. rdzeni transformatorów oraz półtwarde (magnetyczne nośniki informacji).
Nie ulega wątpliwości, że siły magnetyczne są jednymi z podstawowych oddziaływań w naturze. Zachodzą one za pośrednictwem pola magnetycznego, wytwarzanego w skali makroskopowej na skutek ruchu nośników ładunku elektrycznego, czyli np. podczas przepływu prądu elektrycznego. Stały prąd elektryczny powoduje powstanie niezmiennego w czasie pola magnetycznego, podczas gdy prąd zmienny wywołuje nierozerwalnie związane z nim zmienne pola magnetyczne i elektryczne, które razem nazywamy polem elektromagnetycznym.
Warto się jednak zastanowić, co jest źródłem istnienia pola magnetycznego na poziomie subatomowym.
W tej skali wspomniane pole powstaje głównie na skutek ruchu orbitalnego elektronów oraz ich spinu - dominujące znaczenie ma ten ostatni. Wpływ ruchu protonów i neutronów na pole magnetyczne w większości przypadków można pominąć.
Wypadkowy moment magnetyczny atomu jest sumą wszystkich momentów magnetycznych elektronów. Przyroda wykazuje tendencję dążenia do najniższego możliwego stanu energetycznego - z tego powodu pojedyncze momenty magnetyczne (zarówno spinowe, jak i orbitalne) ustawiają się najczęściej w przeciwnych kierunkach. Powoduje to oczywiście wzajemne znoszenie się momentów magnetycznych sparowanych elektronów. Jeśli w danym atomie wszystkie elektrony są sparowane, to nie wykazuje on zewnętrznego momentu magnetycznego. Natomiast w przypadku, kiedy atom posiada pewną ilość niesparowanych elektronów można obserwować zewnętrzny moment magnetyczny, którego wartość zależy w przeważającej mierze od ilości tych elektronów [1].
Znamy dziś oczywiście bardzo wiele różnych źródeł pola magnetycznego. Jednym z największych, a jednocześnie bardzo nam bliskim, jest nasza planeta – Ziemia.
Ziemskie pole magnetyczne występuje naturalnie wewnątrz i wokół Ziemi. Można je przybliżyć poprzez pole dipola magnetycznego z jednym biegunem w pobliżu geograficznego bieguna północnego i z drugim w pobliżu bieguna południowego. Linia łącząca bieguny geomagnetyczne jest nachylona do osi obrotu planety o kąt około 10°. Wokół Ziemi na kilkadziesiąt tysięcy kilometrów rozciąga się tzw. magnetosfera, czyli obszar działania ziemskiego pola magnetycznego.
Należy pamiętać, że zgodnie z przyjętą konwencją geomagnetyczny biegun północny znajduje się w pobliżu geograficznego bieguna południowego Ziemi i vice versa. Wiemy, że przeciwne bieguny magnetyczne się przyciągają, więc północny koniec igły kompasu rzeczywiście wskazuje z pewnym przybliżeniem północny biegun geograficzny, czyli jednocześnie geomagnetyczny biegun południowy.
Dawniej uważano, że powstawanie ziemskiego pola magnetycznego jest spowodowane namagnesowaniem głęboko położonych warstw skalnych zawierających rudy żelaza (np. magnetyt). Na początku XX wieku Piotr Curie wykazał jednak, że wszystkie znane substancje tracą swe właściwości ferromagnetyczne po ogrzaniu ich powyżej pewnej temperatury. Temperatura ta jest charakterystyczna dla każdej substancji ferromagnetycznej i została nazwana temperaturą Curie [2]. Jako że temperatura wnętrza Ziemi jest dużo wyższa niż temperatury Curie substancji, z których jest zbudowane, to namagnesowanie nie może być odpowiedzialne za pole magnetyczne całej planety.
Dziś uważa się, że pole magnetyczne Ziemi najprawdopodobniej wywołują wirowe prądy elektryczne płynące w metalicznym jądrze Ziemi - jest to tak zwana teoria samowzbudnego dynama lub geodynama. Siłą napędową geodynama może być konwekcja zachodząca w płynnym jądrze Ziemi.
Natężenie pola magnetycznego Ziemi zmierzył już Carl Friedrich Gauss w pierwszej połowie XIX wieku. Z późniejszych pomiarów dowiedzieliśmy się, że pole magnetyczne naszej planety jest dynamiczne – jego parametry zmieniają się w sposób powolny, ale nieustanny.
Myślę, że Szanowny Czytelnik nie będzie miał nic przeciwko by samemu spróbować dokonać pomiaru indukcji ziemskiego pola magnetycznego. W tym celu trzeba będzie zbudować prosty przyrząd pomiarowy.

Przyrząd do pomiaru indukcji ziemskiego pola magnetycznego
Budowa przyrządu nie jest skomplikowana i można go wykonać przy wykorzystaniu powszechnie dostępnych materiałów. Jego budowę schematycznie w dwóch prostopadłych do siebie rzutach przedstawia Rys.1.
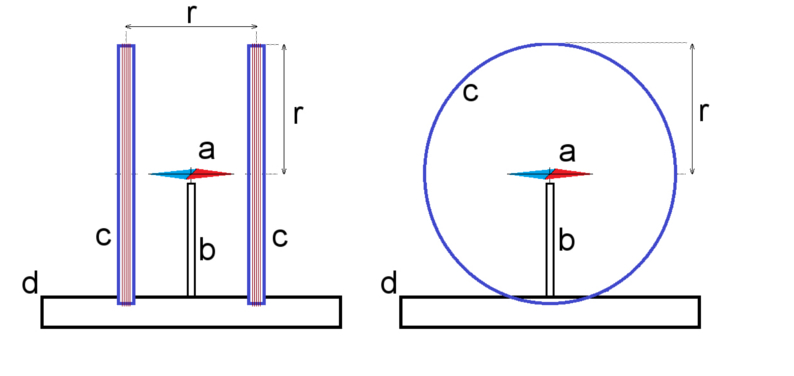
Przyrząd składa się z igły magnetycznej a (wziętej od dowolnego kompasu) umieszczonej na kolumience b osadzonej w podstawie d. Na podstawie są umieszczone także dwie pierścieniowe cewki c, wykonane z kilkudziesięciu zwojów cienkiego drutu izolowanego. Ważne jest, by obie cewki miały te same wymiary i aby znajdowały się w odległości równej promieniowi r każdej z nich. Igła magnetyczna musi być umiejscowiona na linii łączącej środki obu cewek, dokładnie w połowie odległości między nimi. Przedstawiony układ uzwojeń nazywa się cewką Helmholtza.
Poza igłą magnetyczną żaden z elementów przyrządu nie może być zbudowany z materiałów ferromagnetycznych.
Rozmiar cewek powinien być odpowiednio większy od wykorzystanej igły magnetycznej. Na ich karkasy dobrze nadają się okrągłe pokrywki z tworzywa sztucznego zamykające np. puszki kawy (Fot.1).
Wnętrze dwóch takich pokrywek trzeba oczywiście wyciąć, tak by pozostało samo obrzeże (Fot.2).
Na obrzeżu każdej wyciętej pokrywki należy następnie nawinąć np. 20 zwojów drutu miedzianego o średnicy 0,2mm w emalii. Nawinięcie musi być bardzo staranne, czyli zwój przy zwoju – dla obu cewek w tym samym kierunku (Fot.3).
Liczba zwojów nie jest krytyczna – musi być ona jednak taka sama w przypadku obu cewek. Do dalszych obliczeń będziemy musieli znać tę liczbę (oznaczymy ją jako n). Uzwojenie trzeba zabezpieczyć przed rozwinięciem poprzez pomalowanie bezbarwnym lakierem.
Podstawę urządzenia można wykonać z kolejnej dużej zakrętki lub pokrywki z tworzywa sztucznego. Pośrodku należy zaznaczyć punkt, w którym zostanie osadzona kolumienka igły magnetycznej, zaś po jej obu stronach wyciąć otwory, w których zostaną umieszczone wykonane uprzednio cewki (Fot.4).
Cewki należy następnie wkleić w otwory i połączyć je szeregowo, tzn. koniec pierwszej cewki z początkiem drugiej. Połączenia wykonuje się pod spodem postawy, a wolne końce obu cewek wyprowadza się na zewnątrz. Kolumienkę można wykonać z odcinka rurki plastikowej wyciętej np. z długopisu. Trzeba ją wkleić do otworu w podstawie, a na jej szczycie umieścić oś obrotu igły magnetycznej, np. w postaci szpilki, na której igła będzie mogła się swobodnie obracać. Pamiętać należy o dobraniu odpowiedniej wysokości kolumienki, tak by igła znajdowała się w geometrycznym środku układu dwóch cewek (Fot.5).
Ostatnim etapem pracy jest osadzenie na kolumience skali kątowej (np. wydrukowanej i naklejonej na kartonową tarczę) oraz samej igły magnetycznej. Tarczę jest dobrze umocować w taki sposób, by mogła się ona obracać z delikatnym oporem – nie może ona jednak hamować ruchu igły magnetycznej. Gotowy przyrząd w dwóch ujęciach przedstawia Fot.6.
By jednak móc wykorzystać opisany przyrząd musimy się zastanowić nad teoretycznymi podstawami jego działania.
Nieco matematyki
Podstawy matematyczne proponowanej metody pomiaru nie są skomplikowane [3]. Dla ułatwienia ich zrozumienia postaram się przedstawić je krok po kroku.
Przyspieszenie a dla wychylenia x w ruchu drgającym jest określone wzorem 1.
| a=-ω2x | (1) |
Wiedząc, że pulsacja ω jest powiązana z częstotliwością ν zależnością ν=ω/2π otrzymujemy, że
| a=-4ν2π2x | (2) |
Natomiast dla ruchu obrotowego analogiczne równanie pozwalające na obliczenie przyspieszenia kątowego ε dla określonego kąta α przyjmie postać
| ε=-4ν2π2α | (3) |
Dociekliwy Czytelnik z pewnością zauważy, że zawieszoną na osi igłę magnetyczną możemy potraktować jako bryłę sztywną, a działający na nią moment siły M, w zależności od jej momentu bezwładności Ι przyjmie wartość
| M=Ιε | (4) |
Jednocześnie dla określonego momentu magnetycznego μ igły, zawieszonej w polu magnetycznym o indukcji B i wychylonej o kąt α zachodzi równość
| M=-μBsinα | (5) |
co dla niewielkich wartości kąta, dla których sinus jest praktycznie równy temu kątowi (sinα≈α) upraszcza się do postaci
| M=-μBα | (6) |
Zależność ta dowodzi, że jest to ruch harmoniczny, ponieważ moment siły jest proporcjonalny do wychylenia, przy współczynniku proporcjonalności równym k=μB.
Korzystając z zależności 3, 4 i 6 możemy stwierdzić, że
| μB=4ν2π2Ι | (7) |
Znając więc moment magnetyczny oraz moment bezwładności igły magnetycznej, a także mierząc częstotliwość jej drgań w polu magnetycznym możemy wyznaczyć wartość indukcji tego pola!
Czytelnikowi, który już zacierał dłonie z chęci do wyznaczenia indukcji ziemskiego pola pewnie zrzedła mina…
- Jak w prosty sposób wyznaczyć moment magnetyczny i moment bezwładności igły magnetycznej? – zapyta pewnie z nadzieją.
- Nie trzeba tego robić w ogóle! – odpowiem z wysokości mojego biurka.
Rzeczywiście nie są nam potrzebne te dwie wielkości. Jest to sprzyjająca okoliczność, ponieważ w warunkach domowych czy szkolnych nie byłoby łatwo ich wyznaczyć. Ale coś za coś - by pozbyć się wspomnianych zmiennych należy znowu użyć matematyki. Oprócz indukcji ziemskiego pola magnetycznego Bz do pomocy trzeba zaprząc dodatkowe pole o indukcji Bd. Kierunek pola o indukcji Bd musi być w tym przypadku równoległy do pola ziemskiego. Wypadkowa indukcja pola B oddziałującego z igłą, w zależności od zwrotu indukcji będzie określona jako
| B↑= Bz +Bd (zwroty wektorów zgodne) | (8) |
| B↓= Bz -Bd (zwroty wektorów przeciwne) | (9) |
Podstawiając wzory 8 i 9 do zależności 7, otrzymujemy
| μ (Bz +Bd)= 4ν↑2π2 Ι | (10) |
| μ (Bz -Bd)= 4ν↓2π2 Ι | (11) |
Teraz wystarczy zależności 10 i 11 podzielić stronami i uporządkować, by uzyskać
| Bz =Bd (ν↑2+ν↓2/ν↑2-ν↓2) | (12) |
Jak widzimy, rzeczywiście udało się wyeliminować wielkości μ oraz Ι. Wyznaczenie indukcji ziemskiego pola magnetycznego Bz sprowadza się więc do pomiaru częstotliwości drgań ν↑ i ν↓, odpowiednio przy zgodnym i przeciwnym do ziemskiego zwrocie indukcji Bd.
Pozostaje jeszcze konieczność wytworzenia dodatkowego pola magnetycznego i wyznaczenia jego indukcji Bd. Właśnie dlatego w zbudowanym przyrządzie pomiarowym igłę umieściliśmy wewnątrz cewki Helmholtza.
Cewka Helmholtza jest to, jak mogliśmy się już przekonać, układ dwóch zwojnic, który w swoim wnętrzu zapewnia stosunkowo jednorodne pole magnetyczne. Znaczy to, że obrębie tego układu istnieje relatywnie duża przestrzeń o w przybliżeniu stałym wektorze indukcji magnetycznej (Rys.2) [4].
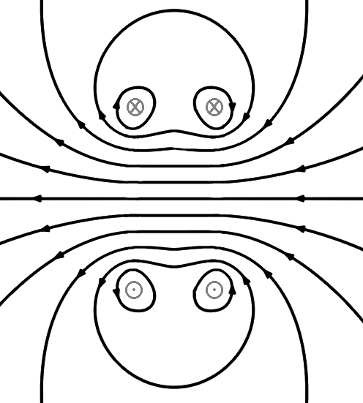
Indukcję pola magnetycznego Bd cewki Helmholtza o n zwojach i promieniu r, przez którą płynie prąd o natężeniu J można wyznaczyć na podstawie prawa Biota-Savarta i jest ona opisana wzorem
| Bd= μ0nJ * 8/5r√5 | (13) |
Podstawiając powyższe równanie do otrzymanej uprzednio zależności 12, otrzymujemy
| Bz =(ν↑2+ν↓2/ν↑2-ν↓2) * μ0nJ * 8/5r√5 | (14) |
Wreszcie! Matematyczna batalia się zakończyła, a zwycięstwo należy do nas. Na polu boju pozostały jedynie łatwe do wyznaczenia zmienne. Wystarczy zmierzyć promień r, policzyć ilość zwojów n oraz wyznaczyć częstotliwości drgań igły ν↑ i ν↓ przy przeciwnych kierunkach przepływu prądu. Pomiaru natężenia prądu J płynącego przez cewkę dokonamy za pomocą amperomierza lub miernika uniwersalnego. Pozostaje jeszcze kwestia tajemniczego współczynnika μ0. Jest to przenikalność magnetyczna próżni będąca stałą o wartości 12,57*10-7 Vs/Am.
Przypomnę: przy opisanej wyżej metodzie ważne jest aby linie sił ziemskiego pola magnetycznego i pola wytwarzanego przez cewkę były do siebie równoległe!
Przy wykorzystaniu zbudowanego urządzenia można wykonać pomiar indukcji także w oparciu o inną metodę przedstawioną schematycznie na Rys.3. W niezaburzonym ziemskim polu magnetycznym Bz igła przyjmuje pozycję równoległą do linii sił tego pola (Rys.3A). Jeśli wytworzymy dodatkowe pole magnetyczne Bd w kierunku prostopadłym (a więc inaczej niż w poprzedniej metodzie) do pola ziemskiego, to na igłę będzie działała siła wypadkowa. Spowoduje ona odchylenie igły o pewien kąt α (Rys.3B).
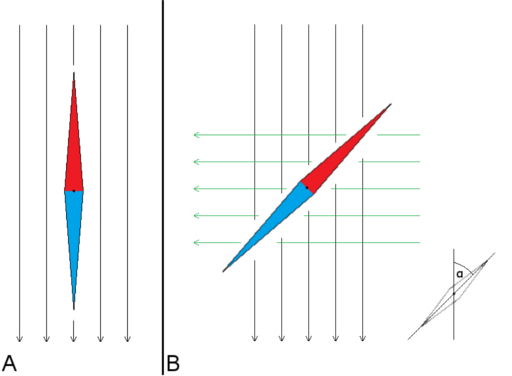
Sięgając do trygonometrii stwierdzamy, że
| ctgα=Bz /Bd | (15) |
Nam zależy oczywiście na uzyskaniu wartości indukcji ziemskiego pola magnetycznego Bz , natomiast Bd wytworzymy ponownie przy wykorzystaniu cewki Helmholtza. Mamy stąd, że
| Bz = ctgα * μ0nJ * 8/5r√5 | (16) |
Dokonując więc pomiaru kąta α o jaki wychyli się igła magnetyczna w wyniku przepływu prądu J przez cewkę Helmholtza składającą z dwóch zwojnic po n zwojów możemy także wyznaczyć indukcję ziemskiego pola magnetycznego Bz .
Pomiary
Przy wykorzystaniu pierwszej metody pomiaru rzeczą jaką należy zrobić na początku jest ustawienie przyrządu na płaskiej wypoziomowanej powierzchni w taki sposób, by igła wskazując północ leżała na linii łączącej środki zwojnic (Fot.7).
Następnie należy zbudować prosty obwód elektryczny łącząc szeregowo cewkę Helmholtza, źródło prądu stałego o napięciu kilku woltów (np. 4 połączone szeregowo ogniwa 1,5V), potencjometr o odpowiednio dobranej oporności (najczęściej 1kΩ) oraz miernika natężenia prądu na zakresie miliamperów. Ja wykorzystałem miernik uniwersalny pozwalający na pomiar natężenia prądy z dokładnością do setnych części miliampera. Przydatny jest także przełącznik kierunku przepływu prądu w cewce, ale można sobie poradzić bez niego – wystarczy w miarę potrzeby zamieniać ręcznie miejscami styki źródła napięcia.
Jako, że wektory indukcji Bz i Bd przy odpowiednim ustawieniu przyrządu powinny mieć ten sam kierunek, to po podłączeniu prądu do cewek nie powinniśmy zaobserwować żadnego wychylenia igły magnetycznej. Nie należy stosować zbyt dużych wartości natężenia prądu J, ponieważ wartość Bd może wtedy okazać się większa od Bz – w takim przypadku wypadkowa siła zmusi igłę do ustawienia się w przeciwnym niż zwykle kierunku, a jej północny koniec nie będzie już wskazywał geograficznej północy. Nie uniemożliwia to pomiarów, ale w pewnym stopniu je utrudnia.
Po ustaleniu się wartości natężenia prądu należy wprawić igłę w delikatne drgania poprzez jej ostrożne popchnięcie w płaszczyźnie poziomej – amplituda drgań nie powinna być zbyt duża, ponieważ w takim przypadku nie będziemy mieli już do czynienia z drganiami harmonicznymi. Teraz trzeba wyznaczyć okres drgań T. Najprościej zrobić to mierząc stoperem czas np. 10 pełnych drgań, a następnie dzieląc wynik przez ich ilość. Potem przy tej samej wartości natężenia prądu J odwracamy kierunek jego przepływu i ponownie mierzymy okres drgań igły.
Procedurę tę powtarzamy dla kolejnych wartości natężeń prądu J. Oczywiście najlepiej wykonać większą ilość pomiarów, po czym je uśrednić.
Wiedząc, że częstotliwość ν jest odwrotnością okresu T uzyskane wartości T↑ i T↓ przeliczamy do ν↑ i ν↓. Dane należy podstawić do wzoru (14) i obliczyć Bz .
Przykładowe wyniki przeprowadzonego przeze mnie doświadczenia przedstawia Tab.1 (n=20; r=0,052m).
| J[A] | (ν↑2+ν↓2)/(ν↑2-ν↓2) | Bz [nT] |
| 0,00501 | 11,69 | 20260,45 |
| 0,00710 | 8,34 | 20484,31 |
| 0,01532 | 3,89 | 20616,04 |
| 0,01988 | 2,89 | 19875,18 |
| 0,03011 | 1,95 | 20311,51 |
Na podstawie uzyskanych danych możemy stwierdzić, że wyznaczone wartości Bz są we wszystkich przypadkach zbliżone do siebie. Średnio Bz jest równe 20309,50nT z odchyleniem standardowym s=251,22nT.
W przypadku drugiej metody przyrząd należy także ustawić na płaskiej powierzchni, ale w taki sposób, aby igła wskazując północ była ustawiona równolegle do płaszczyzny cewek (Fot.8A).
Ponownie zestawiamy taki sam układ elektryczny jak w przypadku poprzedniej metody. Włączenie przepływu prądu J powoduje wychylenie igły magnetycznej o pewien kąt α w stronę zależną od kierunku przepływu prądu (Fot.8B). Powtarzamy pomiar dla zróżnicowanych wartości natężenia, tak by móc uśrednić wynik. Efekty moich pomiarów (wartości n, r bez zmian) przedstawia Tab.2.
| J[A] | α[°] | Bz [nT] |
|---|---|---|
| 0,00409 | 4 | 20233,76 |
| 0,00713 | 7 | 20088,28 |
| 0,01211 | 12 | 19709,09 |
| 0,01931 | 18 | 20559,05 |
| 0,03069 | 27 | 20836,65 |
Jak widać, także w tym przypadku możemy stwierdzić, że wyznaczone wartości Bz są we wszystkich pomiarach zbliżone do siebie. Po uśrednieniu uzyskujemy Bz=20285,37nT z odchyleniem standardowym s=387,92nT.
Wartości indukcji Bz ziemskiego pola magnetycznego wyznaczone przy wykorzystaniu obu metod są do siebie bardzo podobne – uśredniona wartość z pomiarów obiema metodami wynosi 20297,44nT.
Czy na pewno poprawnie?
Aby ponad wszelką wątpliwość potwierdzić przydatność proponowanych metod pomiaru Bz należy odwołać się do danych uzyskanych przez innych. Potrzebne informacje można pozyskać z odpowiedniej literatury i przedstawić je np. w postaci mapy rozkładu interesującej nas wielkości (Rys.4) [5].
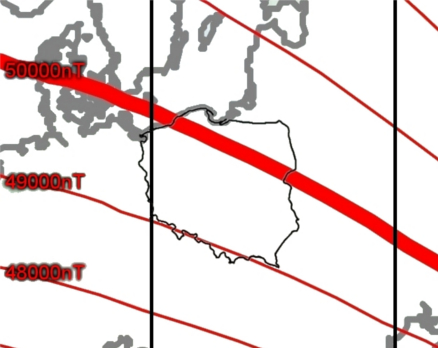
Pomiaru dokonywałem w miejscu położonym w południowej Polsce - odpowiednia wartość odczytana z mapy wynosi więc w przybliżeniu 49000nT. Jest to wartość ponad dwukrotnie wyższa niż uzyskana przez nas! Czyżby więc nasze pomiary były błędne, mimo że obie metody wykazały tak do siebie zbliżone wartości? By móc na to odpowiedzieć należy zrozumieć, jaką konwencję przyjęto w celu wyrażania wielkości związanych z ziemskim polem magnetycznym.
Na większości obszaru Ziemi linie sił naturalnego pola magnetycznego nie przebiegają równolegle do powierzchni planety. W każdym punkcie przestrzeni pole magnetyczne można scharakteryzować wektorem natężenia pola magnetycznego. Do jego opisu w większości przypadków stosuje się sferyczny układ współrzędnych. Należy wtedy określić dla każdego interesującego nas wektora inklinację, deklinację i moduł natężenia. Deklinacją nazywamy kąt między składową poziomą modułu natężenia a południkiem geograficznym, natomiast inklinacją kąt jaki tworzy wektor natężenia pola z płaszczyzną poziomą (Rys.5).
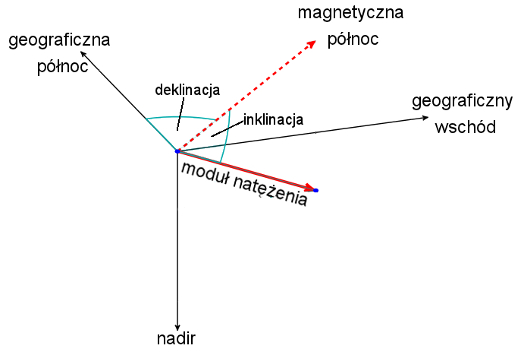
Zauważmy, że w czasie naszych pomiarów pominęliśmy całkowicie inklinację pola magnetycznego, więc mierzyliśmy jedynie składową poziomą indukcji ziemskiego pola magnetycznego Bz . Wartość odczytana z Rys.4 wyraża natomiast moduł tej wielkości. By móc porównać te dwie wartości potrzebujemy wiedzy na temat wielkości kąta inklinacji w miejscu pomiaru (Rys.6).
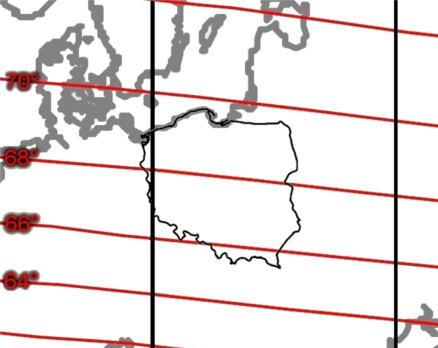
Dla miejsca, w którym dokonywałem pomiaru kąt ten wynosi około 66°. Składowa pozioma indukcji ziemskiego pola magnetycznego wynosi więc w tym przypadku Bz ' = 49000nT * cos 66° = 19930,10nT.
Uzyskana z pomiaru wartość składowej poziomej indukcji ziemskiego pola magnetycznego Bz i wyznaczona z danych literaturowych wartość Bz ' są do siebie bardzo zbliżone. Błąd bezwzględny wynosi jedynie 367,34nT, natomiast względny 1,84%.
Oczywiście na precyzję pomiaru ma wpływ wiele czynników, np. dokładność wykonania przyrządu, obecność dodatkowych pól magnetycznych i obecność dużych mas metalicznych zniekształcających ziemskie pole magnetyczne. Myślę jednak, że biorąc pod uwagę prostotę i łatwość wykonania proponowanego przyrządu trzeba stwierdzić, że umożliwia on zadziwiająco dokładne pomiary indukcji ziemskiego pola magnetycznego. Można go oczywiście przystosować także do pomiaru indukcji innych pól magnetycznych.
Literatura:
- [1] Rubakov V. A., Classical theory of gauge fields, Princeton University Press, 2002, str. 54 – 55, 207 – 208 powrót
- [2] Ples M, Silnik cieplno-magnetyczny, Młody Technik, 1(2015), Wydawnictwo AVT, Warszawa, str. 74 – 75 powrót
- [3] Gaj J., Laboratorium fizyczne w domu, Wydawnictwa Naukowo-Techniczne, Warszawa, 1985 powrót
- [4] Ramsden E., Hall-effect sensors: theory and applications (2nd ed.), Elsevier/Newnes, Amsterdam, 2006, str. 195 powrót
- [5] Maus S., Macmillan S., McLean S., Hamilton B., Thomson A., Nair M., Rollins C., The US/UK World Magnetic Model for 2010-2015, NOAA Technical Report NESDIS/NGDC, 2010 powrót
Wszystkie fotografie i rysunki zostały wykonane przez Autora.
Marek Ples







