Równanie Bernoulliego i lewitująca piłeczka
Prawo Bernoulliego jest jednym z podstawowych równań hydrodynamiki płynów idealnych. Zostało sformułowane przez Daniela Bernoulliego w 1738 roku.
Prawo to obowiązuje dla założeń:
- ciecz nie jest lepka,
- ciecz jest nieściśliwa,
- przepływ jest stacjonarny i bezwirowy
Równanie wtedy przyjmuje postać:
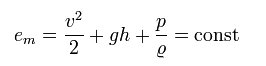
gdzie:
em - energia jednostki masy płynu,
rho - gęstość płynu,
v - prędkość płynu w rozpatrywanym miejscu,
h - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna,
g - przyspieszenie grawitacyjne,
p - ciśnienie płynu w rozpatrywanym miejscu.
Rozpatrując równanie nasuwa się pewien wniosek: jeśli rozpatrujemy rurę o zmiennym przekroju, w której płynie nieściśliwa ciecz w sposób laminarny to logicznym jest, że prędkość przepływu będzie większa w miejscu, gdzie ta rura ma mniejszy przekrój. Pociąga to za sobą mniej intuicyjny efekt. Ciśnienie w cieczy jest mniejsze tam gdzie przepływ jest szybszy czyli w zwężeniu rury! Jest to tak zwany paradoks hydrodynamiczny.
Doświadczenie
Weźmy piłeczkę ping-pongową. Jest ona na tyle lekka, że nadaje się do naszego eksperymentu. Potrzebujemy jeszcze źródła sprężonego powietrza. Najlepszy byłby odkurzacz starego typu, w którym do wylotu powietrza można podłączyć odpowiednią rurę. Nadaje się też suszarka do włosów (o jak największej mocy nadmuchu). Skierujmy strumień poruszającego się z dużą szybkością powietrza w góre i umieśćmy w nim piłeczkę. Zacznie się ona unosić w strumieniu powietrza. Widać to na moim filmiku:
Jak to wyjaśnić? Powietrze jest dobrą analogią płynu idealnego więc z rozsądnym przybliżeniem możemy zastosować tutaj powyższe równanie. Powietrze z odkurzacza porusza się z dużą prędkością wobec otaczającego strumień powietrza. Powoduje to spadek ciśnienia wewnątrz strumienia. Różnica ciśnień między wnętrzem strumienia, a otaczającym powietrzem utrzymuje piłeczkę wewnątrz niego.
Życzę miłej i pouczającej zabawy:)
Literatura dodatkowa:
- Babinsky H., How do wings work?, Physics Education, 2003, 38(6), str. 497-503
- Bukowski J., Mechanika Płynów, Warszawa, 1968
Marek Ples