Interferencja fal akustycznych
Interferencja fal akustycznych
Czym jest interferencja? Każdy z nas słyszał to słowo i często kojarzy się ono w jakiś nieokreślony sposób z falami lub drganiami. Fizyk jednak jednoznacznie stwierdzi, że to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal(elektromagnetycznych, mechanicznych, de Broglie itd.), we wszystkich ośrodkach, w których mogą rozchodzić się dane fale.
Obowiązuje tutaj tak zwana zasada superpozycji fal, która mówi, że amplituda fali wypadkowej A powstałej w wyniki nakładania się fal cząstkowych w każdym punkcie dana jest wzorem:
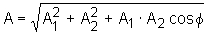
gdzie: A1, A2 - amplitudy fal cząstkowych, φ - różnica faz obu fal.
Jak widzimy, fala wypadkowa może mieć maksymalnie wartość A=A1+A2 dla φ=2k. Fazy obu fal w takim przypadku są idealnie zgodne: odpowiadające sobie punkty fal cząstkowych występują w tych samych miejsach przestrzeni(grzbiet pokrywa się z grzbietem fali, dolina z doliną), w tym samym czasie. Amblituda fali wypadkowej jest więc sumą amplitud fal cząstkowych. Obserwujemy wtedy wzmocnienie. Dla faz przeciwnych(φ=2k+1) wartość amplitudy fali wypadkowej będzie minimalna. Opisuje ją wtedy wzór A=A1-A2. Fale są przesunięte w fazie, nakładają się przecistawne elementy fali (grzbiety z dolinami). Obserwujemy wtedy wygaszenie fali. Jeśli obie fale cząstkowe mają taką samą amplitudę to amplituda fali wypadkowej jest A=0.
Prostym sposobem wytworzenia fal akustycznych o ściśle dobranej częstotliwości i fazie jest wykorzystanie komputera i odpowiedniego programu. Jest wiele generatorów programowych, my jednak postąpimy odrobinę nietypowo i wykorzystamy program Audacity, będący narzędziem do obróbki muzyki. Program ten jest zaawansowanym i wielościeżkowym edytorem plików dźwiękowych. Jest rozpowszechniany na licencji GNU GPL (możliwość darmowego ściągnięcia z sieci). Program dostępny jest w wersjach dla wielu systemów operacyjnych: Unix/Linux, Microsoft Windows i Mac OS.
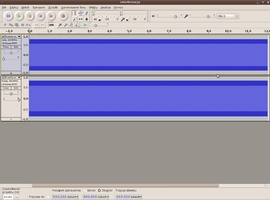
Po ściągnięciu i zainstalowaniu programu potrzebujesz jeszcze pliku projektu, który dla Ciebie przygotowałem. Możesz go pobrać stąd. Po rozpakowaniu archiwum otrzymasz folder, w którego wnętrzu znajdziesz między innymi plik interferencja.aup. Gdy go poklikniesz powinien się uruchomić program audacity z załadowanymi dwoma przebiegami akustycznymi. Powinno to wyglądać mniej więcej tak:
Widzimy dwa przebiegi akustyczne. Jeden z nich(górny) jest przeznaczony dla lewego głośnika, zaś dolny to kanał prawy. Do odtworzenia dźwięku służy zielony przycisk play, umieszczony na górnej belce. Zauważmy, że częstotliwości tych dźwięków różnią się: dla kanału lewego przeznaczona jest częstotliwość 440Hz, zaś dla prawego 441Hz. Widzimy więc, że między częstotliwościami dźwieków płynących z każdego głośnika jest różnica 1Hz. Poziom sygnału jest jak widać jednorodny-przez cały czas trwania dźwięku jego amplituda jest stała na obu kanałach. Włączmy głośniki oraz odtwarzanie. Czy słyszany przez nas dźwięk jest jednorodny? Otóż nie! Wyraźnie słyszymy następujące po sobie momenty wzrostu głośności dźwięku i jej spadku. Po dokładniejszym przysłuchaniu się możemy stwierdzić, że między dwoma chwilami spadku amplitudy(lub jej wzrostu) upływa czas jednej sekundy. Czyli momenty te występują z częstotliwością 1Hz(raz na sekundę). Nie jest przypadkiem, że ta częstotliwość jest równa różnicy obu generowanych częstotliwości. Dlaczego?
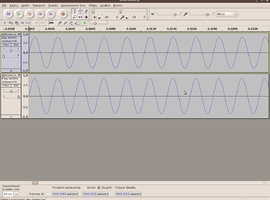
Zastanówmy się skąd biorą się słyszane przez nas różnice głośności dźwięku. Przecież do każdego z głośników dopływa jednostajny sygnał, bez jakichkolwiek wahań amplitudy. Można to sprawdzić wyciszając jeden z kanałów-słyszymy wtedy jednostajny dźwięk. Stąd wniosek, że głośność zmienia się dzięki oddziaływaniu na siebie obu częstotliwości. By dowiedzieć się co jest tego powodem użyjmy narzędzia powiększenia przebiegów(niewielka lupa z plusem na górnej belce). Powiększmy przebieg do momentu kiedy będziemy mogli dojrzeć tworzącą go sinusoidę:
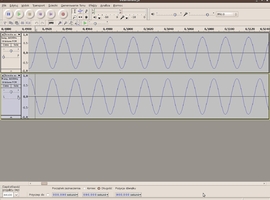
Widzimy dwie podręcznikowe sinusoidy (ich częstotliwości różnią się minimalnie więc nie widać tutaj tego zbytnio w tym momencie). Obie fale mają tą samą fazę początkową(w t=0s, co widać na belce czasu nad przebiegami). Widzimy wyraźnie, że grzbiety fal(oraz ich doliny) występują w tych samych momentach, czyli zgodnie z tym co napisałem wcześniej następuje wzmocnienie(wypadkowa amplituda rośnie). Zauważmy, że te przebiegi nie mają idealnie równej częstotliwości: dolny ma nieco większą częstotliwość czyli grzbiety jego sinusoidy nieznacznie wyprzedzają grzbiety górnej. Tutaj to jeszcze nie ma znaczenia. Przewińmy jednak dolnym suwakiem do t=0,5s(połowa okresu przy f=1Hz). Oto jaki mamy wtedy obraz:
Sytuacja zmieniła się radykalnie. Teraz przebiegi są w przeciwfazie(grzbiet nakłada się z doliną i odwrotnie). Amplitudy się odejmują, czego efektem jest wygaszenie fali(radykalny spadek głośności).
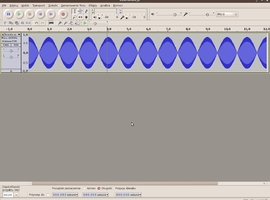
Efekty te powtarzają się naprzemiennie co sekundę(sprawdź!). Daje to częstotliwość zmian równą jednemu hercowi. Zgodnie z tym co zobaczyliśmy przed chwilą, częstotliwość ta będzie zawsze częstotliwością będącą różnicą częstotliwości obu przebiegów. Obie częstotliwości składowe interferując dały falę wynikową o częstotliwośći drgań 1Hz. Możemy to udowodnić: zsumujemy wychylenia obu sinusoid od położenia równowagi. Aby to zrobić otwieramy menu ścieżki(po lewej stronie górnego przebiegu, należy nacisnąć na czarny trójkącik przy nazwie ścieżki), i wybieramy opcję "utwórz ścieżkę stereo". Następnie z górnego menu ścieżki-ścieżka stereo do mono. Program zsumuje amplitudy, czyli zrobi to o czym mówiliśmy przed chwilą. Otrzymamy coś takiego:
Potwierdza to nasze ustalenia. Amplituda zmienia się z częstotliwością 1Hz, w pełnych sekundach obserwujemy maksymalne wzmocnienie, zaś między nimi wygaszenie. Zasada superpozycji jest więc w mocy. Na poniższej animacji możemy obejrzeć szczegółowo zachodzącą tutaj sytuację: czerwony i niebeski przebieg to fale cząstkowe(kanał lewy i prawy), zaś czarna to fala wynikowa.
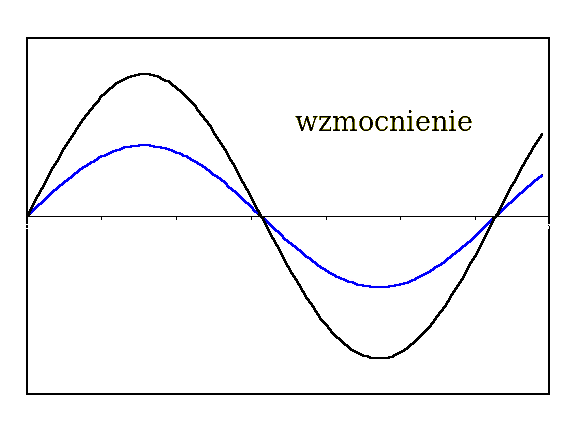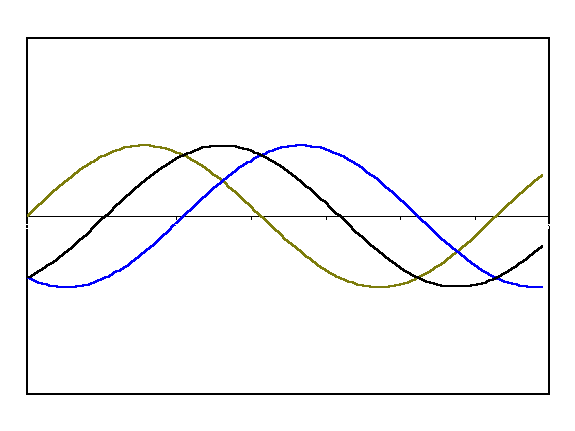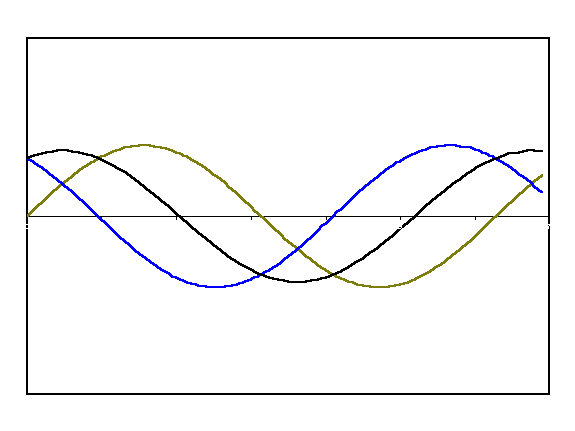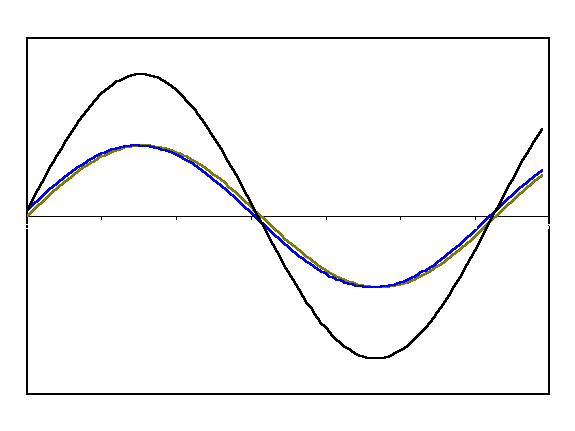
Zjawiska, które tu zaobserwowaliśmy zachodzą także w przypadku wszystkich innych fal.
Życzę miłej i pouczającej zabawy:)
Literatura dodatkowa:
- Born M., Wolf E., Principles of Optics, Cambridge University Press, Cambridge, 1999
- Longhurst R.S., Geometrical and Physical Optics, Longmans, Londyn, 1968
- Resnick R., Halliday D., Fizyka t.1, wydanie IX, Państwowe Wydawnictwo Naukowe, Warszawa, 1993
Marek Ples