Weird Science

Gyroscopic effect

Polish ver­sion is here

The gyro­sco­pic effect is the abi­lity of a rota­ting body to main­tain its orien­ta­tion in space due to the con­se­rva­tion of angu­lar momen­tum. This prin­ci­ple, first descri­bed by Jean Fou­cault in 1852, is fun­da­men­tal to navi­ga­tion and sta­bi­lity sys­tems.

An instru­ment that demon­stra­tes gyro­sco­pic effects is cal­led a gyro­scope. It con­si­sts of a disk that, once set into rapid rota­tio­nal motion, main­ta­ins the ori­gi­nal orien­ta­tion of its axis of rota­tion. Small devia­tions are cau­sed by pre­ces­sio­nal move­ments, which are either acco­un­ted for when deter­mi­ning direc­tion or eli­mi­na­ted thro­ugh dam­ping.

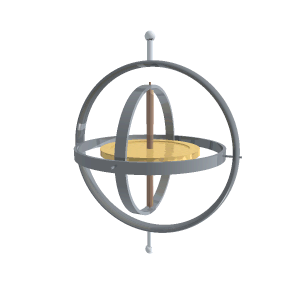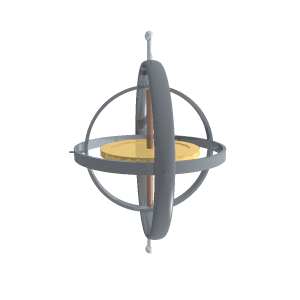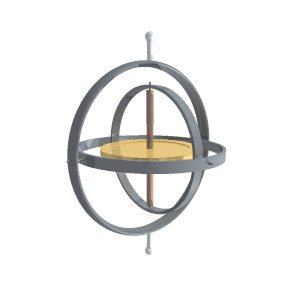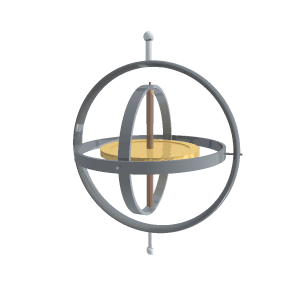
Ilustracja

Source: http://upload.wiki­me­dia.org/wiki­pe­dia/com­mons/d/d5/Gyro­scope_ope­ra­tion.gif
acces­sed: Janu­ary 20, 2012

A rota­ting body with limi­ted fre­e­dom of motion of its rota­tio­nal axis (for exam­ple, fixed along one of the axes of the Car­te­sian coor­di­nate sys­tem) is cal­led a top. A gyro­scope is also refer­red to as a free top.

Gyro­sco­pes are used to con­struct gyro­com­pas­ses, which have wide­spread appli­ca­tions in navi­ga­tion and in devi­ces used to indi­cate a selec­ted direc­tion in air­pla­nes, heli­cop­ters, ships, and so on. A device built on this prin­ci­ple is cal­led a gyro­scope, a gyro­com­pass, or a gyro­sco­pic com­pass. A gyro­scope is also moun­ted in a gyro­the­o­do­lite to deter­mine the geo­gra­phic azi­muth.

Fun fact: The beha­vior of a gyro­scope direc­tly results from the prin­ci­ple of con­se­rva­tion of angu­lar momen­tum, so many rota­ting bodies exhi­bit gyro­sco­pic pro­per­ties. These inc­lude cele­stial bodies! Any cele­stial body rota­ting aro­und its axis exhi­bits the gyro­sco­pic effect and, con­se­qu­en­tly, pre­ces­sion. For Earth, the period of pre­ces­sion is 25,920 years.

Let’s con­duct a sim­ple expe­ri­ment demon­stra­ting the gyro­sco­pic effect.

What Do We Need?

First, we need a gyro­scope. Any well-balan­ced fly­wheel can serve this func­tion. You can use a fly­wheel from a non-func­tio­ning tape recor­der:

Ilustracja:

Kliknij, aby powiększyć

We could spin it using our musc­les, but we’ll do it dif­fe­ren­tly. We will mount it on the shaft of a small elec­tric motor. We need a motor with sha­fts pro­tru­ding from both sides. Press the gyro­scope onto the shaft on one side after first remo­ving its ori­gi­nal axle:

Ilustracja:

Kliknij, aby powiększyć

Con­nect the motor to a power source using thin, fle­xi­ble wires. Then, hol­ding the motor in your hand, apply vol­ta­ge­—the gyro­scope’s disk will start to spin. After rea­ching its maxi­mum rota­tio­nal speed, gen­tly place the gyro­scope on the shaft pro­tru­ding from the oppo­site side. The gyro­scope will not fall over, even if you give it a sli­ght push. The motor, con­ti­nu­o­u­sly main­ta­i­ning the disk’s high speed, pre­vents the entire assem­bly from tip­ping over. The rota­ting fly­wheel resi­sts any force attemp­ting to change its orien­ta­tion because alte­ring the direc­tion of its angu­lar momen­tum vec­tor requ­i­res torque. This resi­stance mani­fe­sts as the gyro­sco­pic effect, allo­wing the device to main­tain balance even when sub­jec­ted to exter­nal for­ces like gra­vity.

Note: The rota­tio­nal speed of the gyro­scope is typi­cally mea­su­red in revo­lu­tions per minute (RPM). For exam­ple, if the disk spins at 5,000 RPM, this cor­re­sponds to about 523.6 radians per second. (For refe­rence, 1 RPM ≈ 0.10472 rad/s.) If neces­sary, you can also convert rota­tio­nal speed to impe­rial units: 5,000 RPM ≈ 523.6 rad/s or appro­xi­ma­tely 83.33 rota­tions per second.

In this expe­ri­ment, the gyro­sco­pic effect is easily obse­rva­ble because the angu­lar momen­tum gene­ra­ted by the spin­ning disk resi­sts chan­ges in orien­ta­tion, demon­stra­ting the fun­da­men­tal prin­ci­ple behind gyro­sco­pic sta­bi­lity used in navi­ga­tion and engi­ne­e­ring appli­ca­tions.

Fur­ther rea­dings:

Marek Ples

Aa